Probability density function

Boxplot and probability density function of a normal distribution Template:Nowrap.

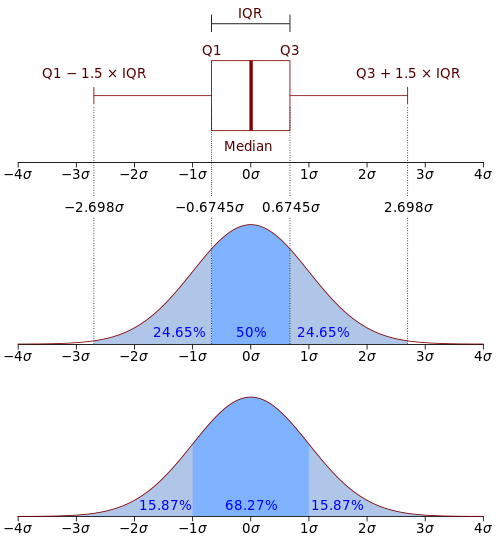
In probability and statistics, a probability density function is a function that characterizes any continuous probability distribution. For a random variable X, the probability density function of X is sometimes written as $f_X(x)$. The integral of the probability density function in the interval $[a,b]$ yields the probability that a given random variable with the given density is contained in the interval provided. By definition, the probability density function is non-negative throughout its domain, on which the integral sums up to 1.

Probability density versus probability mass function

The probability mass function is to a discrete probability distribution what the probability density function is to a continuous probability distribution. The probability density function is necessary to be able to work with continuous distributions.

A random variable with a continuous probability distribution can take on any value within that distribution. Casting a dice will give the numbers 1 to 6, with a probability of $\frac{1}{6}$, but this is not a continuous function, as only the numbers 1 to 6 are possible.

In contrast, two people will not have the same height or the same weight. Using a probability density function, it is possible to determine the probability for people between Template:Convert and Template:Convert, or between Template:Convert and Template:Convert, even though there are infinitely many values between these two bounds.